61
paldados com base em estudos complementares.
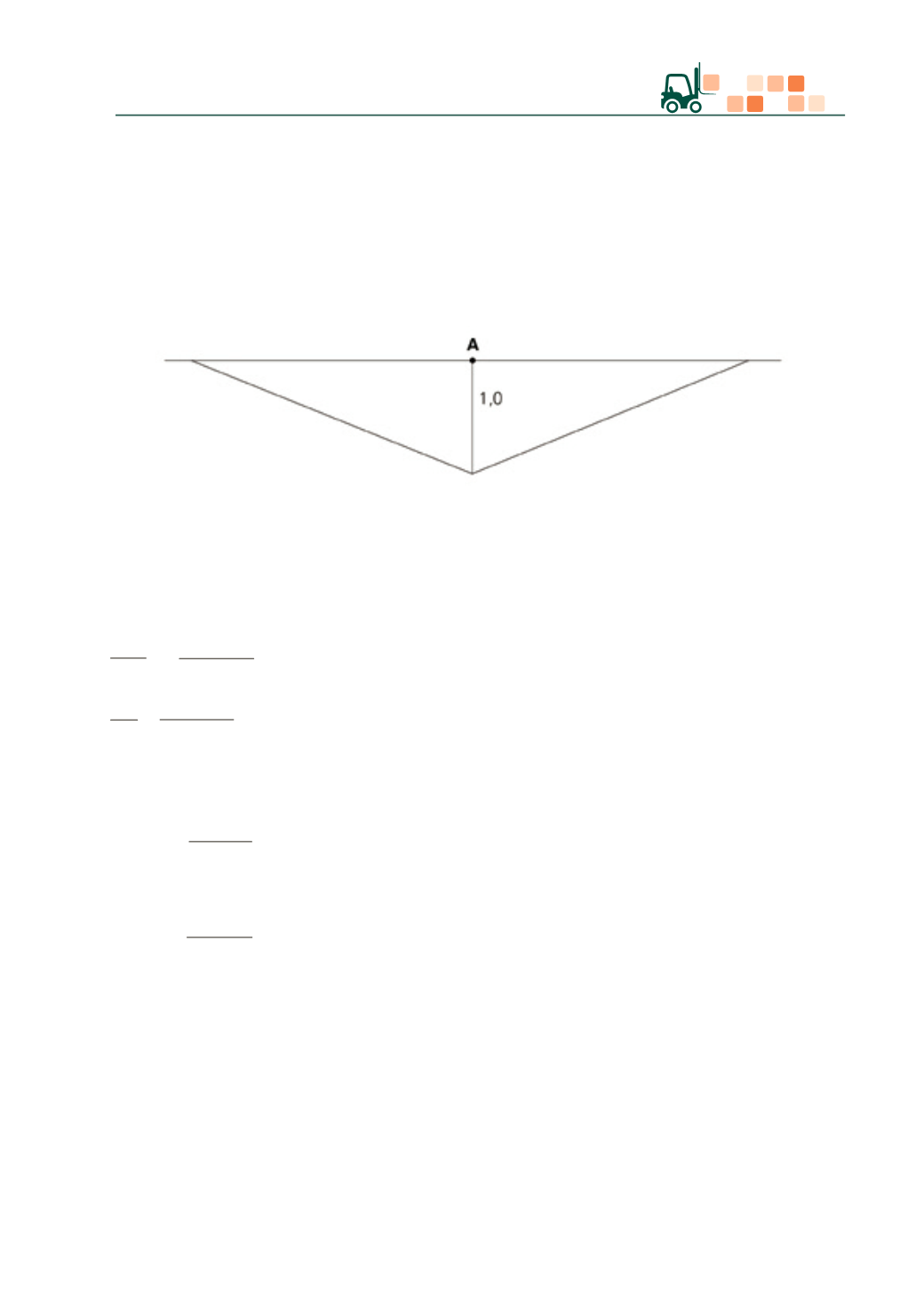
Uma vez determinado
R
c
, o cálculo das cargas contribuintes é bastante simples quando assumimos
distribuição triangular, sendo máxima no ponto considerado (
A
) e zero em
R
c
(
figura
5.3
).
Na
figura
5.3
, as cargas
P1
,
P4
e
P5
estão fora da zona de contribuição, não incrementando as
tensões em
A
; embora possam promover uma redução, devido aos momentos negativos que elas
possam gerar no ponto
A
, esse fato só é considerado em condições especiais.
Figura 5.3
Na
figura
5.2
, as cargas
P1
,
P4
e
P5
estão fora da zona de contribuição, não incrementando as
tensões em
A
. Embora essas cargas possam contribuir para a redução do esforço em
A
, devido
ao momento negativo que geram na placa, essa condição não é, na maioria dos casos, levada em
consideração.
As cargas contribuintes geradas por
P2
e
P3
podem ser calculadas por semelhança de triângulo:
=
(n
x
ℓ - X
2
) ;
γ
2
n
x
ℓ
1
=
(n
x
ℓ - X
3
)
γ
3
n
x
ℓ
1
C
2
= P
2
C
3
= P
3
e
n
x
ℓ - X
2
n
x
ℓ - X
3
n
x
ℓ
n
x
ℓ
(
(
(
(
Portanto:
A soma das cargas
C
2
e
C
3
gera uma carga equivalente que substitui, na seção
A
, os
P2
e
P3
,
produzindo o mesmo esforço.
Novamente analisando a
figura
5.2
se
P2
=
P3
, a seção do pavimento mais solicitada irá se loca-
lizar imediatamente abaixo de
P2
ou
P3
ou ainda a meia distância delas, devendo as duas seções
serem pesquisadas; mas se
P2
≠
P3
a seção mais solicitada poderá ocorrer em qualquer ponto
entre as duas cargas e a pesquisa deve ser mais abrangente.
O mesmo conceito pode ser empregado para outros tipos de carregamento e é muito útil, por exem-
plo, para cargas lineares. Neste caso, podemos discretizar a carga linear em várias cargas pontuais
e se escolhermos distâncias infinitamente pequenas, a carga equivalente, após a integração, será o


