Pavimentos Industriais de Concreto Armado
60
5.2.1 – Cargas Contribuintes
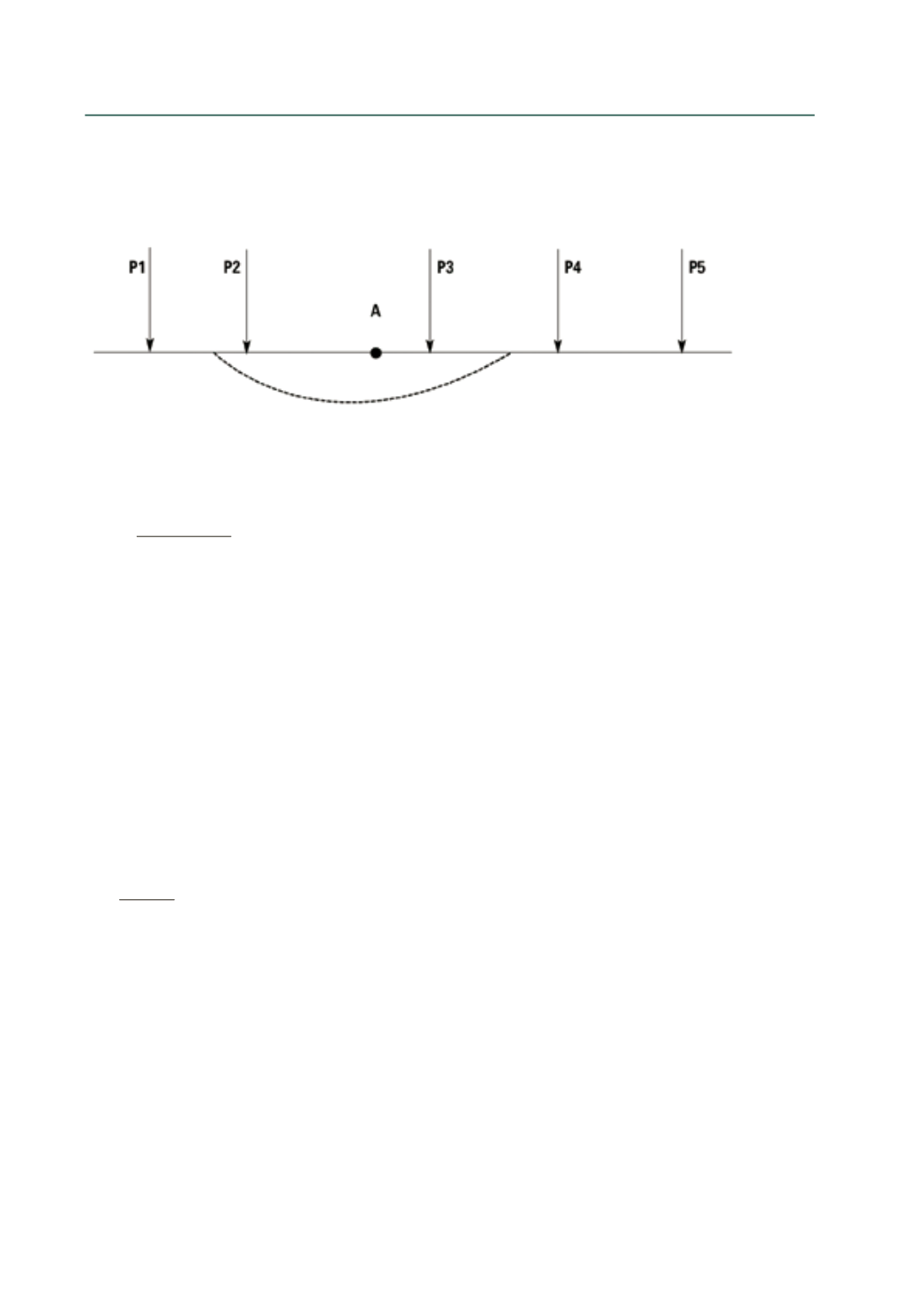
Considere-se o ponto
A
da figura
5.2
. Cada carga situada a uma determinada distância deste ponto
irá produzir nele um determinado esforço, função direta da sua posição relativa.
Figura 5.2
No plano cartesiano, podemos representar um círculo de influência
RC
dentro do qual qualquer car-
regamento irá promover um incremento em
A
. O diâmetro desse círculo é função do raio de rigidez,
que é dado pela expressão:
ℓ =
E x h
3
12(1-μ
2
) x k
0,25
(
(
onde:
ℓ
é o raio de rigidez (m)
E
é o módulo de elasticidade do concreto (Pa)
H
é a espessura da placa de concreto (m)
μ
é o coeficiente de Poisson do concreto
k
é o coeficiente de recalque (Pa/m)
Observe que na fórmula do raio de rigidez está embutido o momento de inércia da placa de con-
creto, dado pela expressão:
ℓ = b x h
3
12
Sendo h a altura do piso e b a largura, normalmente considerando-se uma faixa unitária. Essa infor-
mação é importante quando desejamos levar em consideração o espraiamento de tensões citado
em item
5.1
, pois o momento de inércia da seção armada diminui na medida em que a fissuração
da seção aumenta.
Entretanto, essa análise mais aprofundada foge do escopo deste trabalho mas essas informações
estão disponíveis na bibliografia deste trabalho
(Rodrigues,
2003)
.
Voltando a questão das cargas contribuintes, o raio de influência, a partir de
A
é dado por:
R
c
= N x ℓ
N
pode variar de 1 a 2 e sua escolha é opção do projetista. Valores inferiores a 1,5 devem ser res-


