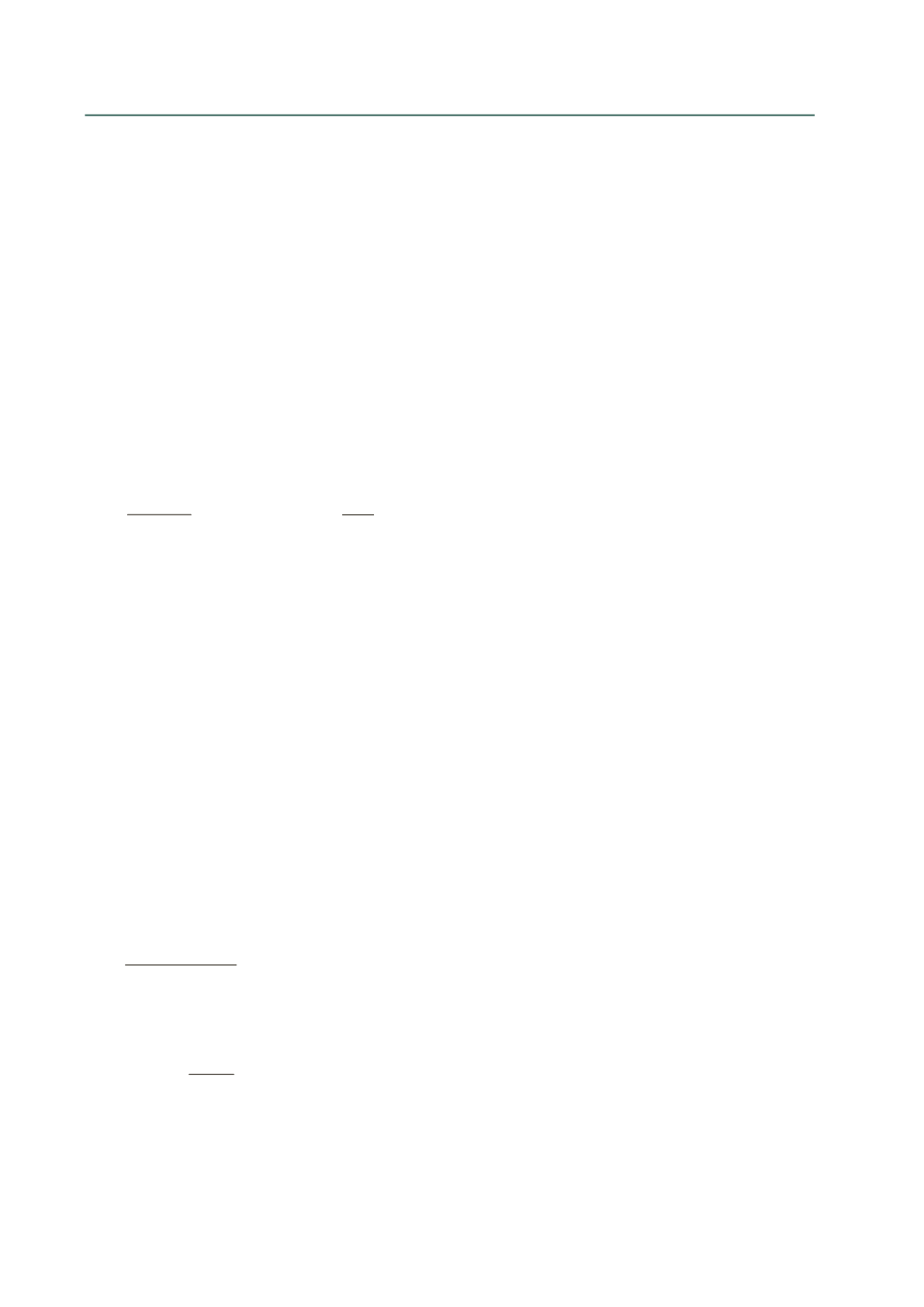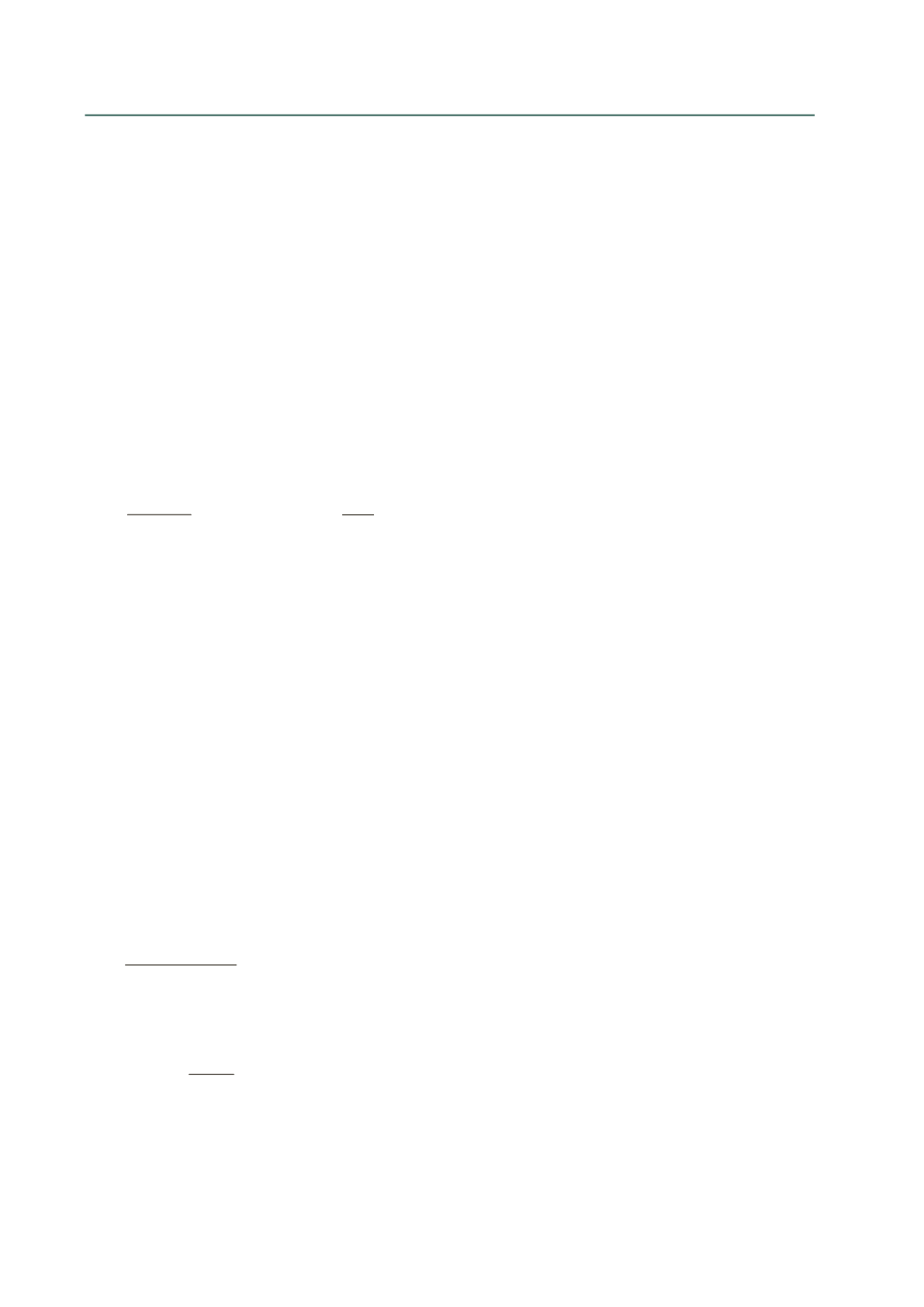
Pavimentos Industriais de Concreto Armado
78
5.5.2 Pavimentos Estruturalmente Armados
É o modelo clássico de dimensionamento, similar as estruturas de concreto armado (
Rodrigues
e
Pitta,
1997
), desenvolvido per Losberg (
Losberg,
1961
), que determinou experimentalmente a
validade do conceito de que o momento resistente total é formado pela soma dos momentos ne-
gativo e positivo.
De modo similar ao que foi visto no item anterior, o momento negativo é dado somente pela re-
sistência do concreto e o positivo, pela tela soldada, agora posicionada na face inferior da placa,
aumentando consideravelmente o braço de alavanca da armadura, dado por (
h
–
c
), sendo
c
o
cobrimento inferior da armadura, geralmente 3 cm.
A armadura necessária para resistir ao um determinado momento fletor pode ser determinada por
processos analíticos ou programas desenvolvidos em planilhas eletrônicas; não dispondo desses
recursos a taxa de aço é facilmente obtida também por meio dos coeficientes adimensionais
k
6
e
k
3
(
Santos,
1983
), por meio das expressões:
k
6
=
A
S
=
k
3
x
b x d
2
e
M
k
M
k
d
Por facilidade de uso, devemos empregar as unidades em cm para
b
(largura útil, tomada como 100
cm) e
d
(d = h – 3cm, ou adotando outro cobrimento) e para o momento fletor
M
k
,
tf.cm
.
Os adimensionais
k
6
e
k
3
são correlacionáveis com o emprego da
figura
5.22
. Nela já estão intro-
duzidos os coeficientes de minoração dos materiais – 1,4 para o concreto e 1,15 para o aço – e
também o coeficiente de majoração das ações de 1,4. Cabe ao projetista decidir se eles são ade-
quados ou alterá-los de acordo com as necessidades do projeto.
Por exemplo, vamos supor um piso com 15 cm de espessura, submetido a um momento fletor M=
150 tf.cm (12 kN.m/m); os demais dados são os mesmos do exemplo de aplicação do
item
5.5.1
.
Deste modo, M
neg
= 78,75 tf.cm.
M
res
= M
neg
+ M
pos
M
pos
= M
res
+ M
neg
M
pos
= 150 - 78,75 = 71,25tf.cm
k
6
=
= 205
71,25
100 x (15 - 3)
2
Da
figura
5.21
, k
3
é aproximadamente 0,277, portanto:
A
s
= 0,277 x
= 1,52cm
2
/m
13
71,25